第4回　流れのシミュレーション（数値計算というアプローチ）

私は研究者としてのキャリアを水理学の研究から始めました。水理学をご存じでしょうか。水や空気といった流体の流れの運動を明らかにする流体力学を用い、川や海、地球の水の流れとその結果生じる物質やエネルギーの伝達を研究する学問で、観測と実験、そして理論（数値計算）の3方向からアプローチします。

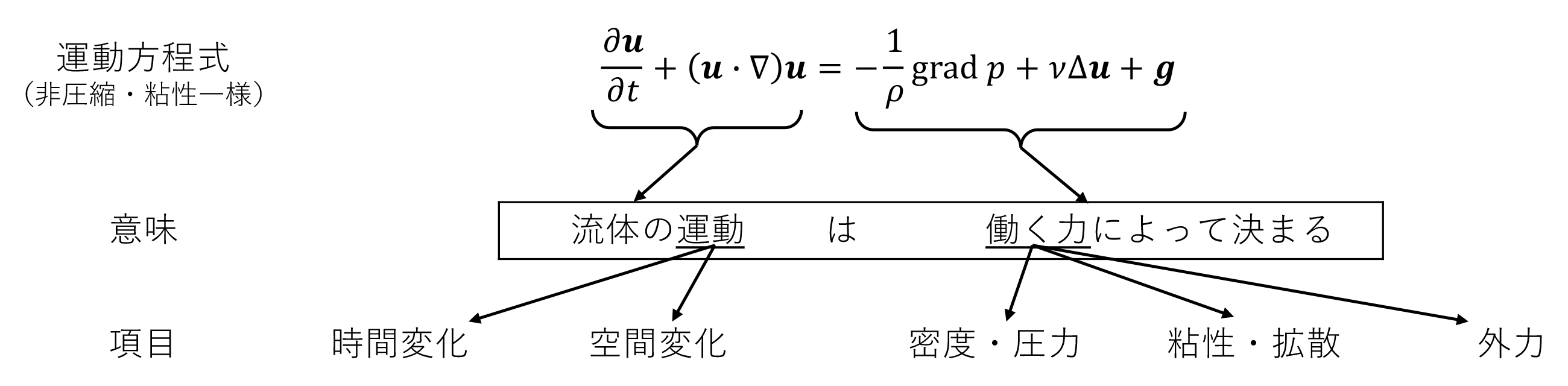
機会があったら、観測や実験についても深掘りしたいところですが、今回のメインは理論とその解法となる数値計算についてです。物理現象である流れにはその運動を表す運動方程式が与えられています。有名なのはナビエ・ストークス方程式と呼ばれ、海の水のように圧縮されず、粘性が一定と仮定できる場合には、図1のように書くことができます。なにやら怪しげな演算子が一杯ですが、内容には立ち入らず、大胆に注釈すると、左辺第一項が流れ u の時間変化、第二項が流れ u により運ばれる水の空間的な移動量（移流項）、右辺第一項は密度 ρ により生じる圧力、第二項が粘性 ν による拡散、第三項が重力や表面張力、海底摩擦などの外力を表しています。一言で言えば「流体の運動は働く力によって決まっている」と読むことができます。通常はこの運動方程式と合わせて質量保存則である連続方程式も併用して流れを解くことになります。

図1：流体の基礎方程式であるナビエ・ストークス方程式の概要

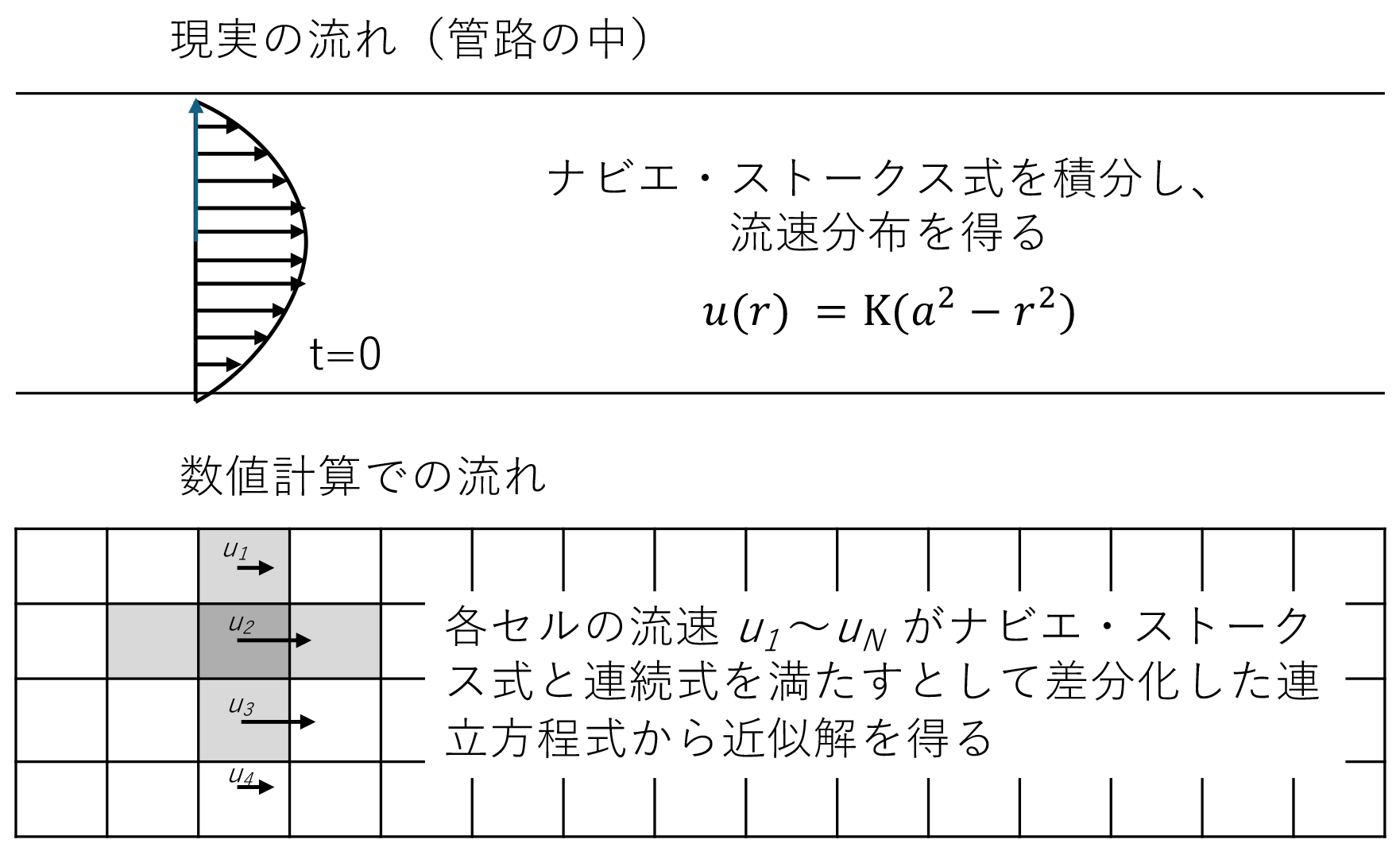
さて、こうした方程式を数値的に解くためには、離散化という方法を使います。方程式は切れ目のない流体の運動を表していますが、数値計算では、ある一定の体積を持った空間（セル）で切り分け、方程式の中にある流れ u の空間変化（空間微分）を、2つのセルの間の流れ u の差 (u_n+1 - u_n) として表します。方程式には時間に関する変化（時間微分）もありますが、同様に、ある時間間隔毎の流速値の差に直せますので、方程式全体が流速値に関する四則演算に置き換えることができます。こうした置き換えを方程式の離散化と言います。

そして、離散化により四則演算に置き換えられた基礎方程式は、流れ u に対する巨大な連立方程式となるので、その解を得ることができるのです。ただし、その連立方程式は巨大であるとともに、多くの係数は0に近いので、その答えを得るには特別なテクニックが必要とされ、できるだけ簡単で正確な解法を求めて、研究者たちがしのぎを削ってきました。

図2：現実の流れと数値計算での流れのイメージ図

離散化されたセルの中では流速や圧力、密度などが一様と仮定しています。実際には、流速 u は定常成分u‾ と乱れ成分 u' を持っており、この u' が不規則に変化するので、そのセルが大きすぎると、正しい流れが再現できません。すなわち、正解に近づけようとすると、より小さなセルと細かい時間間隔が必要となり、より大きな行列を解くこととなり、大容量で高速な計算機が必要となります。

また、運動方程式の右辺の項で示されていた外力については、通常、直接解くことができず、観測値などを用いて値を与えることとなります。これを方程式を解く際の境界条件と呼びますが、実は、その精度が計算の結果を左右するといっても過言ではありません。なので、どんなに大容量で高速に計算しても、全く役に立たない場合もあり得るのです。ですから、計算結果と現地データを見比べて、正しく計算できているかを検証することがとても大切です。数値計算では現実にないケースを計算できることが強みですが、そうした場合には、その検証データが得られないというジレンマも抱えています。

1980年代には、東京湾の流れを2kmのセルで分解して単層の流れを1潮汐分計算するのに大型計算機を用いても、数日かかりました。1990年代以降、そうしたセル内での乱れの強度を別途モデル化する手法が普及し、少ない行列でより正確な計算が可能になるとともに、小型のワークステーションの高速化が相まって、2000年代には、東京湾内の潮流計算も1kmのセルで3層の計算をするのに数時間で済むようになっていました。現在では、パソコンでも同等の速度での計算ができるまでになっています。

そうした動きと並行して、セルの大きさを小さくして、より精密な流れを解いていく方法（直接数値シミュレーション：DNS）や、セルの大きさを境界の凹凸に合わせて変化させる方法（非構造格子）を用いて、より詳細な流れを再現する試みも行われています^1,2。

少し変わった方法では、流れの最小単位をセルではなく渦などの流れの構造に着目する方法（渦法）があります。これは境界要素法と呼ばれる離散化の方法で、流れの中にある渦が相互に引き起こす流れを重ね合わせることで、セル数に縛られずに（ただし渦の数に縛られる）流れの詳細な構造が再現できる方法です。私も、渦の渦法による流れの計算に挑み、潮流により発生する島の背後の渦列を再現することに成功し、なぜ島の背後の洗堀が非対称なのかを解明することができました。

図3：島背後の渦列の形成
（渦法による計算の結果、島の形状の非対称性により両端から発生する
渦の大きさが異なり、洗堀力の違いとなり洗堀深さが非対称になった³）

如何でしょうか。コンピュータの中で神秘的（？）に行われている流れの数値計算の意外な単純さと、そうした手順の中で近似解を得ることの限界もあるのだということが、ちょっとでも伝われば幸いです。

ショートコラム

マングローブ林調査・地球温暖化最前線
（2025年9月）

2025年8月31～9月8日にかけて、南山大学藤本潔教授をリーダーとするミクロネシア連邦ポンペイ島でのマングローブ林観測に参加してきました。この調査は、1994年から30年にわたり藤本教授を始めとする多くのマングローブ林の研究者が継続してプロットと呼ばれる同じ調査区域をポンペイ島内に5か所設定し、そのプロット内の全てのマングローブの樹種・幹の直径を一本一本記録してきたものです。プロットは、大きいもので50m×200mあり、1回で600本を超える木を測定することとなり大変です。幹の直径を測ることで木の地上部の容積が推定でき、有機物の生産量に換算することができるのです。

マングローブ林には、河川や沿岸、陸地から土砂が供給され、そこに根を張り成長していきます。成長する木の根には、細根と呼ばれる小さな根が生えては分解され土になっていくのです。この土の中での炭素蓄積と、潮汐などによる土砂堆積が合わさることで、林の地盤高さが維持されているのですが、地球温暖化による海面上昇により地盤高の維持が難しくなっていくのではないかという懸念があります。

実際、ポンペイ島の一つのプロットでは、マングローブ林内の土壌侵食が進んでおり、根が空中に露出してしまっているところも当該研究チームにより発見されています。効果的な炭素蓄積のための方策検討や土砂循環の実態の解明が待たれています。

ポンペイ島でのオヒルギの巨木と侵食を受けている根
（本来は、膝状の根が10cm程度出るくらいの地盤高となるはずのところ既に40cm程度の侵食が起こっています）

（連載 第5回 へ続く）